January 15, 2009
Another Round Of The Ultimatum Game
Let's see if it's fair this time.
Go ahead and read Part 1, The Ultimatum Game Is A Trap.
My issue is simply that the Ultimatum Game, which supposedly shows a sense of fairness, and is evidence that this fairness is an evolutionary trait that was selected, doesn't necessarily show any of these things.
The premise is that when people play a round of the UG, they generally do not offer a 99/1 split but something more "fair" (e.g. 60/40) and people repeatedly refuse to accept deals that aren't "fair."
Ergo, it is fairness that this game tests, and fairness is what has evolved.
Even if we grant that 60/40 is the ordinary split, why does this mean it is fairness that has been selected for?
An easy counterexample is to rewrite the discussion in terms of envy: in the UG, people rarely offer 99/1 because they know it will be refused-- because they know the other person would just as soon shoot his own foot to spite his hand. And Player 2 would refuse anything less than 70/30 not because it's not fair, but because he is a jealous, deeply spiteful person who hates when other people have more, even if it is fair. Flat tax, anyone? No? Thought not.
I rewrite this all as envy not to show that it is actually envy that the Game tests; or that envy is not evolved, or that even fairness is not evolved; but merely to demonstrate that the outcome of the UG can not be taken to be an example of any specific idea or behavior. People may choose the same results for entirely different reasons. Sales of guns are probably a good example of this.
The best we can say-- and even this isn't completely accurate-- is that the common choices of 60/40 have been selected for; that they multiply disparate and unconnected causes, yet by virtue of their overdetermination, this choice becomes the one humans pick. In other words, what has been selected for is the propensity to choose 60/40. Period. No cause can be inferred.
II.
Let's look at whether the Ultimatum Game and Prisoner's Dilemma actually measure fairness.
A. If it were indeed fairness that was being displayed, then fairness should be immune to the payoff. Whether the pot were a billion dollars, or 6 silver coins, the outcome should be the same. Within cultures, this is generally true. What matters is that the pot consist of something valued, that does not have a self-imposed maximum (e.g. chocolates wouldn't work because there's a point when you actually don't want any more chocolates.)
B. Fairness presupposes an ability to value something. You can't use a pot of dirt, not because it doesn't have any value, but because it is impossible to value consistently (e.g. it may have personal value to one or the other but not a general value.) Also, you expect the representation of that value to be irrelevant, so long as we all know the value. The game can be played with pesos or dollars if I know the conversion rate.
C. The value of something must be economic. Not monetary, necessarily, but in the simplest possible sense, more has to be more and less has to be less.
But, sadly for the evolution of humanity and the hopes of millions who believe they are greater than their history, this is not the case.
III.
Imagine games with a pot of 3 cents, $3, 300 cents, or $300. Look at those carefully. If fairness was at issue, game outcomes should not vary substantially based on the pot. And, if they did, you'd at least expect very similar results for the 300 cents and the $3 pots; they are, after all, the same, and the players are likely not retarded.
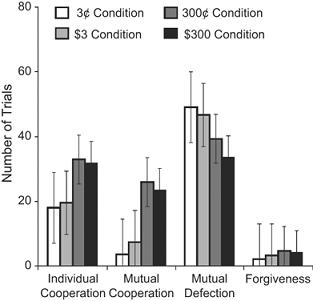
This is the Prisoner's Dilemma, a slightly different game, but the difference is not important here.
Take a look at the results of "mutual cooperation." Not only are they very much dependent on the size of the pot, but they are dependent in a way which makes no sense at all: not based on the amount of money, but the size of the number. 300 (cents) was "bigger" than 3 (dollars.)
Note that the results of 300 cents were in every case more similar to the results of $300 then of $3. Their brains saw 300 cents and 300 dollars as more similar than 3 dollars. (1) I'll save you the trouble of looking it up: none of the players had had strokes.
The interpretation of nearly every UG and PD paper depends on assuming that the players are judging the value of the pot based on monetary value or its conversion, but it is quite apparent that they are (at least also) judging it using some deeper cognitive construct of "amount" or "size-- that here overruled monetary value.
A quick correlate from the stock market: people perceive Google ($300/share) as more expensive than Bank of America ($9)-- that $1000 buys you "more" BoA, even though it's the same $1000 invested either way, and, by most metrics, Google is cheaper.
Given that these cognitive distortions-- and who knows if they're distortions, or don't have some positive value after all?-- exist, how can we believe that a 60/40 split using a $10 pot is an example of "fairness?" Is our sense of fairness so weak (despite millennia of selection) that it can't withstand the presence of a few non-significant zeros?
How do you know these games aren't actually showing you the effect of a single cognitive constraint, and that constraint-- not fairness or cooperation-- is what has been selected for?
IV.
Even if these games did test fairness, why would we think they were defining fairness using Western standards-- which have existed only for a fraction of humanity's history, in only a small part of the world? People have had slaves longer then they have not had slaves, and had no moral problem with it. Is that fair? If the ancient Romans played the Ultimatum Game, would the split be the same? Or, if it was, would it have the same meaning?
To assume the common outcome of 60/40 from a few studies applies to the general population independent of cultural effects; to assume the results are independent of the cognitive distortions of size, number, and value; and to extrapolate these results across different times in history-- is such madness as to border on religion. To then believe this all as the outcome of the natural selection of a single complex behavioral trait is religion.
And to be so mad as to believe we know the nature of this single trait-- to know the the character of the god Fairness-- brings us back to madness again.
------
1 Not only that, but there is a trend towards overestimating 300 cents-- why? Go ahead and imagine 300 cents. That's bigger than $300-- bigger in terms of weight, volume, height, etc.
2 Consider a number line, with numbers labeled one through ten. Now extend the line, place the number 100. Now place the number 1000. Then 10000. Etc. The distance from 1 to 100 is more accurate than your distance from 100 to 1000, and 1000 to 10000. The larger the number, the more difficult it is to accurately.
Similarly, consider getting punched in the face. The perception of the pain is related to you're starting level of pain. A punch that is ten times as hard isn't felt to be exactly ten times as painful.
Not only is the error greater with each successive increse; it turns out that in specific cases, the error follows a mathematically demonstrable progression, namely, that our perception of is proportional to the logarithm of of the stimulus difference.
P=k ln S/So, where So is the lowest possible perceived stimulus (Weber-Fechner law).
I'll let the awesomeness of that sink in for a moment. (3).
Turns out this law may only be applicable in certain cases. For example, the perception of stimulus is also related to other variables like distraction, temperature of the body, etc. And maybe a power function rather than logarithmic function is more applicable. All this is for another day.
3. But here's a perplexing little conundrum. Fechner's law shows that the perception of a physical stimulus is proportional to the logarithm of the magnitude of the physical stimulus. But our perception of magnitude itself-- our perception of numbers-- also follows such a logarithmic function. So choosing a number ("on a scale from one to ten") to describe our perception, that number itself is related to the stimulus by a power function. In other words, the mere act of attempting to quantify a perception adds an additional level of complexity to the problem.
My issue is simply that the Ultimatum Game, which supposedly shows a sense of fairness, and is evidence that this fairness is an evolutionary trait that was selected, doesn't necessarily show any of these things.
The premise is that when people play a round of the UG, they generally do not offer a 99/1 split but something more "fair" (e.g. 60/40) and people repeatedly refuse to accept deals that aren't "fair."
Ergo, it is fairness that this game tests, and fairness is what has evolved.
Even if we grant that 60/40 is the ordinary split, why does this mean it is fairness that has been selected for?
An easy counterexample is to rewrite the discussion in terms of envy: in the UG, people rarely offer 99/1 because they know it will be refused-- because they know the other person would just as soon shoot his own foot to spite his hand. And Player 2 would refuse anything less than 70/30 not because it's not fair, but because he is a jealous, deeply spiteful person who hates when other people have more, even if it is fair. Flat tax, anyone? No? Thought not.
I rewrite this all as envy not to show that it is actually envy that the Game tests; or that envy is not evolved, or that even fairness is not evolved; but merely to demonstrate that the outcome of the UG can not be taken to be an example of any specific idea or behavior. People may choose the same results for entirely different reasons. Sales of guns are probably a good example of this.
The best we can say-- and even this isn't completely accurate-- is that the common choices of 60/40 have been selected for; that they multiply disparate and unconnected causes, yet by virtue of their overdetermination, this choice becomes the one humans pick. In other words, what has been selected for is the propensity to choose 60/40. Period. No cause can be inferred.
II.
Let's look at whether the Ultimatum Game and Prisoner's Dilemma actually measure fairness.
A. If it were indeed fairness that was being displayed, then fairness should be immune to the payoff. Whether the pot were a billion dollars, or 6 silver coins, the outcome should be the same. Within cultures, this is generally true. What matters is that the pot consist of something valued, that does not have a self-imposed maximum (e.g. chocolates wouldn't work because there's a point when you actually don't want any more chocolates.)
B. Fairness presupposes an ability to value something. You can't use a pot of dirt, not because it doesn't have any value, but because it is impossible to value consistently (e.g. it may have personal value to one or the other but not a general value.) Also, you expect the representation of that value to be irrelevant, so long as we all know the value. The game can be played with pesos or dollars if I know the conversion rate.
C. The value of something must be economic. Not monetary, necessarily, but in the simplest possible sense, more has to be more and less has to be less.
But, sadly for the evolution of humanity and the hopes of millions who believe they are greater than their history, this is not the case.
III.
Imagine games with a pot of 3 cents, $3, 300 cents, or $300. Look at those carefully. If fairness was at issue, game outcomes should not vary substantially based on the pot. And, if they did, you'd at least expect very similar results for the 300 cents and the $3 pots; they are, after all, the same, and the players are likely not retarded.

This is the Prisoner's Dilemma, a slightly different game, but the difference is not important here.
Take a look at the results of "mutual cooperation." Not only are they very much dependent on the size of the pot, but they are dependent in a way which makes no sense at all: not based on the amount of money, but the size of the number. 300 (cents) was "bigger" than 3 (dollars.)
Note that the results of 300 cents were in every case more similar to the results of $300 then of $3. Their brains saw 300 cents and 300 dollars as more similar than 3 dollars. (1) I'll save you the trouble of looking it up: none of the players had had strokes.
The interpretation of nearly every UG and PD paper depends on assuming that the players are judging the value of the pot based on monetary value or its conversion, but it is quite apparent that they are (at least also) judging it using some deeper cognitive construct of "amount" or "size-- that here overruled monetary value.
A quick correlate from the stock market: people perceive Google ($300/share) as more expensive than Bank of America ($9)-- that $1000 buys you "more" BoA, even though it's the same $1000 invested either way, and, by most metrics, Google is cheaper.
Given that these cognitive distortions-- and who knows if they're distortions, or don't have some positive value after all?-- exist, how can we believe that a 60/40 split using a $10 pot is an example of "fairness?" Is our sense of fairness so weak (despite millennia of selection) that it can't withstand the presence of a few non-significant zeros?
How do you know these games aren't actually showing you the effect of a single cognitive constraint, and that constraint-- not fairness or cooperation-- is what has been selected for?
IV.
Even if these games did test fairness, why would we think they were defining fairness using Western standards-- which have existed only for a fraction of humanity's history, in only a small part of the world? People have had slaves longer then they have not had slaves, and had no moral problem with it. Is that fair? If the ancient Romans played the Ultimatum Game, would the split be the same? Or, if it was, would it have the same meaning?
To assume the common outcome of 60/40 from a few studies applies to the general population independent of cultural effects; to assume the results are independent of the cognitive distortions of size, number, and value; and to extrapolate these results across different times in history-- is such madness as to border on religion. To then believe this all as the outcome of the natural selection of a single complex behavioral trait is religion.
And to be so mad as to believe we know the nature of this single trait-- to know the the character of the god Fairness-- brings us back to madness again.
------
1 Not only that, but there is a trend towards overestimating 300 cents-- why? Go ahead and imagine 300 cents. That's bigger than $300-- bigger in terms of weight, volume, height, etc.
2 Consider a number line, with numbers labeled one through ten. Now extend the line, place the number 100. Now place the number 1000. Then 10000. Etc. The distance from 1 to 100 is more accurate than your distance from 100 to 1000, and 1000 to 10000. The larger the number, the more difficult it is to accurately.
Similarly, consider getting punched in the face. The perception of the pain is related to you're starting level of pain. A punch that is ten times as hard isn't felt to be exactly ten times as painful.
Not only is the error greater with each successive increse; it turns out that in specific cases, the error follows a mathematically demonstrable progression, namely, that our perception of is proportional to the logarithm of of the stimulus difference.
P=k ln S/So, where So is the lowest possible perceived stimulus (Weber-Fechner law).
I'll let the awesomeness of that sink in for a moment. (3).
Turns out this law may only be applicable in certain cases. For example, the perception of stimulus is also related to other variables like distraction, temperature of the body, etc. And maybe a power function rather than logarithmic function is more applicable. All this is for another day.
3. But here's a perplexing little conundrum. Fechner's law shows that the perception of a physical stimulus is proportional to the logarithm of the magnitude of the physical stimulus. But our perception of magnitude itself-- our perception of numbers-- also follows such a logarithmic function. So choosing a number ("on a scale from one to ten") to describe our perception, that number itself is related to the stimulus by a power function. In other words, the mere act of attempting to quantify a perception adds an additional level of complexity to the problem.
15 Comments