March 12, 2010
Illusionist
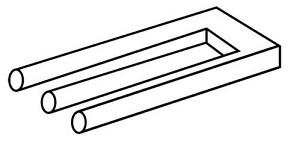 "i agree"
"i agree"
I.
The brain assumes that any two lines which meet must form a plane; specifically, that they do not overlap but separated along a third access by empty space.
But what makes the object an illusion isn't that the lines don't meet-- they do; but that the surfaces-- middle "prong" (starting from the tip and moving back towards the base)-- don't meet. In fact, the surface disappears. The illusion, therefore, is one of constancy: in a static 2D drawing, an object cannot disappear into nothingness.
The parts of the object are perfectly ordinary-- consider the tips vs. the base-- but their union presents a paradox because a static depiction demands change. It asks you to see the prong as both prong and empty space-- that it changes before your eyes. A surface becomes a boundary, and a boundary becomes a surface. It is as if the fork exists in two simultaneous states, an idea which is incompatible with our reality.
II.
"It's an illusion. It's an impossible object."
How is it an illusion? How is it impossible? It's completely possible, I'll draw it myself:
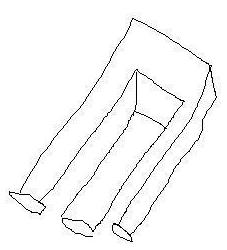
So real is this object that I could teach a blind man to draw it. How can you say it doesn't exist?
The illusion isn't that this 3D object doesn't exist. The illusion is that this object represents a 3D object at all, and that that 3D object doesn't exist. But the 2D drawing certainly exists, and the 2D object is not telling you to see it as a 3D object, the object isn't talking to you. The question you should be asking yourself is why you need to see this as 3D. No sane person looks at this 2D drawing and says it is impossible:

The fork isn't an optical illusion at all; the eye sees perfectly clearly what is before it. This is a cognitive illusion; and, indeed, it isn't even an illusion-- your cognition parses every detail, analytically, interprets the discontinuities as part of a continuum. In short, the cognition knows fully well that what it sees is easily drawn in 2D and impossible to construct in 3D, and knows precisely where the error lies-- and yet it wants wants to see this object-- not any 2D objects, not a scribble ball, but this specific object-- in 3D, despite its better judgment. This isn't involuntary; you can stop any time you want. You want to see this a certain way, and so you choose to do so.
You are being lied to, by yourself.
But what makes the object an illusion isn't that the lines don't meet-- they do; but that the surfaces-- middle "prong" (starting from the tip and moving back towards the base)-- don't meet. In fact, the surface disappears. The illusion, therefore, is one of constancy: in a static 2D drawing, an object cannot disappear into nothingness.
The parts of the object are perfectly ordinary-- consider the tips vs. the base-- but their union presents a paradox because a static depiction demands change. It asks you to see the prong as both prong and empty space-- that it changes before your eyes. A surface becomes a boundary, and a boundary becomes a surface. It is as if the fork exists in two simultaneous states, an idea which is incompatible with our reality.
II.
"It's an illusion. It's an impossible object."
How is it an illusion? How is it impossible? It's completely possible, I'll draw it myself:

So real is this object that I could teach a blind man to draw it. How can you say it doesn't exist?
The illusion isn't that this 3D object doesn't exist. The illusion is that this object represents a 3D object at all, and that that 3D object doesn't exist. But the 2D drawing certainly exists, and the 2D object is not telling you to see it as a 3D object, the object isn't talking to you. The question you should be asking yourself is why you need to see this as 3D. No sane person looks at this 2D drawing and says it is impossible:

The fork isn't an optical illusion at all; the eye sees perfectly clearly what is before it. This is a cognitive illusion; and, indeed, it isn't even an illusion-- your cognition parses every detail, analytically, interprets the discontinuities as part of a continuum. In short, the cognition knows fully well that what it sees is easily drawn in 2D and impossible to construct in 3D, and knows precisely where the error lies-- and yet it wants wants to see this object-- not any 2D objects, not a scribble ball, but this specific object-- in 3D, despite its better judgment. This isn't involuntary; you can stop any time you want. You want to see this a certain way, and so you choose to do so.
You are being lied to, by yourself.
20 Comments